Chapter1. 신경망 복습
1.1. 수학과 파이썬 복습
1.2. 신경망의 추론

- 2층 신경망 입력층/은닉층/출력층 = (X) / (Affine+Sigmoid) / (Affine+S)
- Affine $X \cdot W+B$ : 신경망의 순전파에서 수행하는 행렬의 곱
- Sigmoid $\sigma(x) = {1 \over1+e^{-x}} $ : 비선형 활성화 함수
*추론 과정에서는 출력층에서 굳이 Softmax를 적용시키지 않고 가장 높은 score를 정답으로 판단한다.
1.3. 신경망의 학습

- 2층 신경망 입력층/은닉층/출력층 = (X) / (Affine+Sigmoid) / (Affine+Softmax+Cross Entropy Error+L)
- Softmax $y = {e^{a_k} \over \sum e^{a}}$ : 출력층의 활성화 함수, 다중클래스 분류 문제에서 사용
- Cross Entropy Error
- $L = -\sum t \cdot logy$ : 보통 다중클래스 분류 신경망에서 사용되는 loss function
- Back-propagation
- 덧셈 노드 : gradient distrubutor
- Sum 노드 : gradient distrubutor (N개로)
- 곱셈 노드 : gradient switcher
- 분기 노드 : 기울기들의 합
- Repeat 노드 : 기울기 N개의 합
- MatMul 노드 : ${{\partial L}\over {\partial x}} = {{\partial L}\over {\partial y}}W^T$
- *Repeat $\leftrightarrow$Sum (반대 관계)
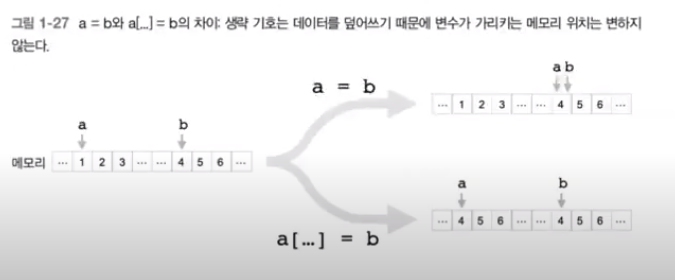
- Deep copy
- 신경망 학습의 순서 (1~3 반복)
- SGD (Stochastic Gradient Descent) 무작위로 선택된 데이터(미니배치)에 대해 기울기를 이용하는 방식
- 1. 미니배치 2. 기울기 계산 3. 매개변수 갱신
1.4. 신경망으로 문제를 풀다
- 1. 신경망 구현
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size):
I, H, O = input_size, hidden_size, output_size
# 가중치와 편향 초기화
W1 = 0.01 * np.random.randn(I, H)
b1 = np.zeros(H)
W2 = 0.01 * np.random.randn(H, O)
b2 = np.zeros(O)
# 계층 생성
self.layers = [
Affine(W1, b1),
Sigmoid(),
Affine(W2, b2)
]
self.loss_layer = SoftmaxWithLoss()
# 모든 가중치와 기울기를 리스트에 모은다.
self.params, self.grads = [], []
for layer in self.layers:
self.params += layer.params
self.grads += layer.grads
def predict(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
def forward(self, x, t):
score = self.predict(x)
loss = self.loss_layer.forward(score, t)
return loss
def backward(self, dout=1):
dout = self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return dout
- 2. 학습용 코드
# 하이퍼파라미터 설정
max_epoch = 300
batch_size = 30
hidden_size = 10
learning_rate = 1.0
# 데이터 읽기, 모델과 옵티마이저 생성
x, t = spiral.load_data()
model = TwoLayerNet(input_size=2, hidden_size=hidden_size, output_size=3)
optimizer = SGD(lr=learning_rate)
# 학습에 사용하는 변수
data_size = len(x)
max_iters = data_size // batch_size
total_loss = 0
loss_count = 0
loss_list = []
for epoch in range(max_epoch):
# 데이터 뒤섞기
idx = np.random.permutation(data_size)
x = x[idx]
t = t[idx]
for iters in range(max_iters):
batch_x = x[iters*batch_size:(iters+1)*batch_size]
batch_t = t[iters*batch_size:(iters+1)*batch_size]
# 기울기를 구해 매개변수 갱신
loss = model.forward(batch_x, batch_t)
model.backward()
optimizer.update(model.params, model.grads)
total_loss += loss
loss_count += 1
# 정기적으로 학습 경과 출력
if (iters+1) % 10 == 0:
avg_loss = total_loss / loss_count
print('| 에폭 %d | 반복 %d / %d | 손실 %.2f'
% (epoch + 1, iters + 1, max_iters, avg_loss))
loss_list.append(avg_loss)
total_loss, loss_count = 0, 0
- Trainer 클래스 fit()은 2(학습용 코드)와 비슷함
class Trainer:
def __init__(self, model, optimizer): # model = 1(TwoLayerNet)
self.model = model
self.optimizer = optimizer
self.loss_list = []
self.eval_interval = None
self.current_epoch = 0
def fit(self, x, t, max_epoch=10, batch_size=32, max_grad=None, eval_interval=20):
data_size = len(x)
max_iters = data_size // batch_size
self.eval_interval = eval_interval
model, optimizer = self.model, self.optimizer
total_loss = 0
loss_count = 0
start_time = time.time()
for epoch in range(max_epoch):
# 뒤섞기
idx = numpy.random.permutation(numpy.arange(data_size))
x = x[idx]
t = t[idx]
for iters in range(max_iters):
batch_x = x[iters*batch_size:(iters+1)*batch_size]
batch_t = t[iters*batch_size:(iters+1)*batch_size]
# 기울기 구해 매개변수 갱신
loss = model.forward(batch_x, batch_t)
model.backward()
params, grads = remove_duplicate(model.params, model.grads) # 공유된 가중치를 하나로 모음
if max_grad is not None:
clip_grads(grads, max_grad)
optimizer.update(params, grads)
total_loss += loss
loss_count += 1
# 평가
if (eval_interval is not None) and (iters % eval_interval) == 0:
avg_loss = total_loss / loss_count
elapsed_time = time.time() - start_time
print('| 에폭 %d | 반복 %d / %d | 시간 %d[s] | 손실 %.2f'
% (self.current_epoch + 1, iters + 1, max_iters, elapsed_time, avg_loss))
self.loss_list.append(float(avg_loss))
total_loss, loss_count = 0, 0
self.current_epoch += 1
def plot(self, ylim=None):
x = numpy.arange(len(self.loss_list))
if ylim is not None:
plt.ylim(*ylim)
plt.plot(x, self.loss_list, label='train')
plt.xlabel('반복 (x' + str(self.eval_interval) + ')')
plt.ylabel('손실')
plt.show()
1.5. 계산 고속화
- 비트 정밀도 넘파이는 64bit 부동소수점 수를 표준으로 사용하나, 신경망의 추론과 학습은 32bit로도 인식률을 거의 떨어뜨리는 일 없이 수행할 수 있다. 메모리 측면, 데이터 병목현상, 계산 속도 등의 이유로 데이터 타입을 32bit로 전환하여 사용한다.
- GPU 딥러닝의 대량의 곱하기 연산을 빠르게 수행할 수 있다. 쿠파이(전용 컴퓨팅, 플랫폼 설치해야함) 등
$\to$ .astype(np.float32) or .astype('f')
'3-2기 스터디 > NLP 입문' 카테고리의 다른 글
| [7주차] 딥러닝을 이용한 자연어처리 입문 Chap.2 텍스트 전처리 (0) | 2022.05.30 |
|---|---|
| [5주차] NLP Chapter 5.2 RNN이란 ~ 6. 게이트가 추가된 RNN (0) | 2022.05.02 |
| [4주차] NLP Chapter 4. word2vec 속도 개선 ~ 5.2 RNN이란 (0) | 2022.05.02 |
| [3주차] NLP Chapter3. word2vec (0) | 2022.04.22 |
| [2주차] NLP Chapter2 - 자연어와 단어의 분산 표현 (0) | 2022.04.11 |



댓글